Applications of quantum algorithms in the resolution of algebraic problems
Physics undergraduate theoretical/computational project, Universidad de los Andes (2021)
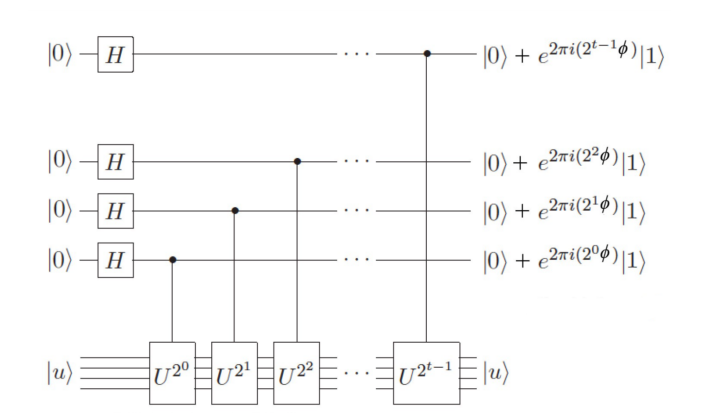
Quantum computing has developed, in recent the decades, several useful tools for solving algebraic problems based on the postulates of quantum mechanics, as well as from fundamental concepts of statistical physics. The possibility of creating computers whose operation is based on the laws of quantum physics, as opposed to classical physics, has aroused great interest and has become an important topic of scientific research. As meritorious examples, the DeustchJosza, Grover and Shor algorithms arrive at specific solutions of situations posed within the theory of statistical mechanics and experimentation, so that a detailed analysis of the most relevant properties of each of these would allow the extraction of new information corresponding to the handling and development of quantum algorithms. In this sense, this theoretical / computational project aims to investigate the techniques used in quantum algorithms to solve numerical, polynomial and probabilistic problems, with respect to basic implementations of quantum circuits in classical and quantum processing units. Furthermore, in order to evaluate the computational power of each developed algorithm, quantifying the precision and processing times is essential for the analytical understanding of the system. The results of this project showed that the amplitude amplification methods, the unstructured search technique, the phase estimation method and the quantum Fourier transform determine the most important algebraic operations of the Deustch-Josza, Grover and Shor algorithms. From examples that go from the double-slit experiment to the transformations of quantum states through their phases, it is verified how the superposition of states and the concept of quantum parallelism is fundamental in the analysis and computation of the probability amplitudes of each cubit. In particular, the Shor algorithm allowed the factorization of the numbers N = 15, N = 35 and N = 65 for both processing units, despite notable differences in the probability of success and the times of success. execution of each system. The applicability of quantum algorithms in classical computers, despite computational errors, is consistent and allows the user to reach results with precision close to 0,5. However, the simulation of the implemented quantum circuit determines polynomial execution times, as expected. In conclusion, quantum algorithms built for solving algebraic problems can be extrapolated to a great variety of physical systems, whether classical or quantum, and can reproduce, with good precision, results at achievable execution times.
Universidad de los Andes | Vigilada Mineducación
Reconocimiento como Universidad: Decreto 1297 del 30 de mayo de 1964.
Reconocimiento personería jurídica: Resolución 28 del 23 de febrero de 1949 Minjusticia.
Web design and programming © Gabriel Téllez
