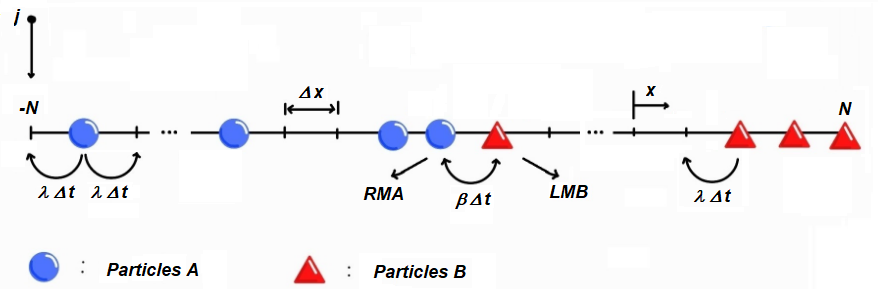
We describe the steady state of the annihilation process of a one-dimensional system of two initially separated reactants A and B. The parameters that define the dynamical behavior of the system are the diffusion constant, the reaction rate, and the deposition rate. Depending on the ratio between those parameters, the system exhibits a crossover between a diffusion-limited (DL) regime and a reaction-limited (RL) regime. We found that a key quantity to describe the reaction process in the system is the probability p(xA, xB) to find the rightmost A (RMA) particle and the leftmost B (LMB) particle at the positions xA and xB, respectively. The statistical behavior of the system in both regimes is described using the density of particles, the gap length distribution xB − xA, the marginal probabilities pA(xA) and pB(xB), and the reaction kernel. For both regimes, this kernel can be approximated by using p(xA, xB). We found an excellent agreement between the numerical and analytical results for all calculated quantities despite the reaction process being quite different in both regimes. In the DL regime, the reaction kernel can be approximated by the probability to find the RMA and LMB particles in adjacent sites. In the RL regime, the kernel depends on the marginal probabilities pA(xA) and pB(xB).