In the present document, a bibliographic review was carried out on the topic of collisions between two solitons, non-linear waves, and the effects of collision on these waves. The focus was exclusively on solitons of the sine-Gordon (s-G) model in two dimensions, one spatial and one temporal.

The starting point was obtaining non-trivial solutions for the s-G equation. For this, the method known as the Bäcklund transformation was employed, which allows for the construction of solutions for differential equations by mapping a known solution for this differential equation and applying integrability conditions. This method leads to simpler differential equations than the original and allows for the construction of a new solution. For the case of the s-G equation, multiples of integers of 2π were used as the starting solution, leading to Kink and Anti-Kink solutions.

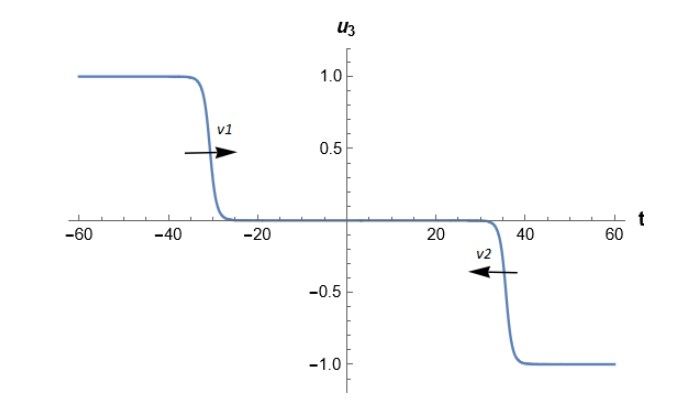
Once the Kink and Anti-Kink solutions were obtained, it was necessary to find a way to construct a solution to the s-G equation as a superposition of these waves in order to study collisions between them. The method for achieving this superposition of solutions is through the Bäcklund transformation, but instead of applying the Bäcklund transformation directly, the Bianchi permutation theorem was employed to find a purely algebraic relationship, making it possible to construct a new non-trivial solution as a superposition of the two previously mentioned solutions, which can give rise to two different types of solutions. The first is a wave formed by the union between a Kink and an Anti-Kink, known as the breather, which oscillates continuously emulating breathing. The second is simply a superposition of these solitons traveling independently through the same medium, allowing for collisions between them.

With the solutions that are a superposition of solitons, collisions of two Kinks and a Kink with an Anti-Kink will be studied, while the remaining cases are not considered, as their analysis and results are analogous to those studied in the document. The way these collisions will be studied is through the individual behavior of the solitons before and after the collision. This is achieved by moving to the moving reference frame of each soliton and studying the asymptotic behavior of the superposition, which should conclude in the appearance of a phase shift in the position of the center of mass for each of the solitons.