Física estadística de fuera de equilibrio de sistemas con interacciones de largo alcance
En este programa de investigación proponemos estudiar aspectos dinámicos de la física estadística de varios sistemas de muchas partículas con interacciones de largo alcance. En sistemas con interacciones de largo alcance, como lo pueden ser sistemas de partículas cargadas, estas interacciones hacen que cada partícula esté fuertemente correlacionada con todas las demás, inclusive las que se encuentran a gran distancia. Esto generalmente complica su estudio y puede llevar a descubrir propiedades interesantes que no ocurren en sistemas con interacciones de corto alcance. Como prototipo de estos sistemas estudiaremos dos modelos en particular: un modelo de fusión de cargas y un modelo de formación de doble capa eléctrica.
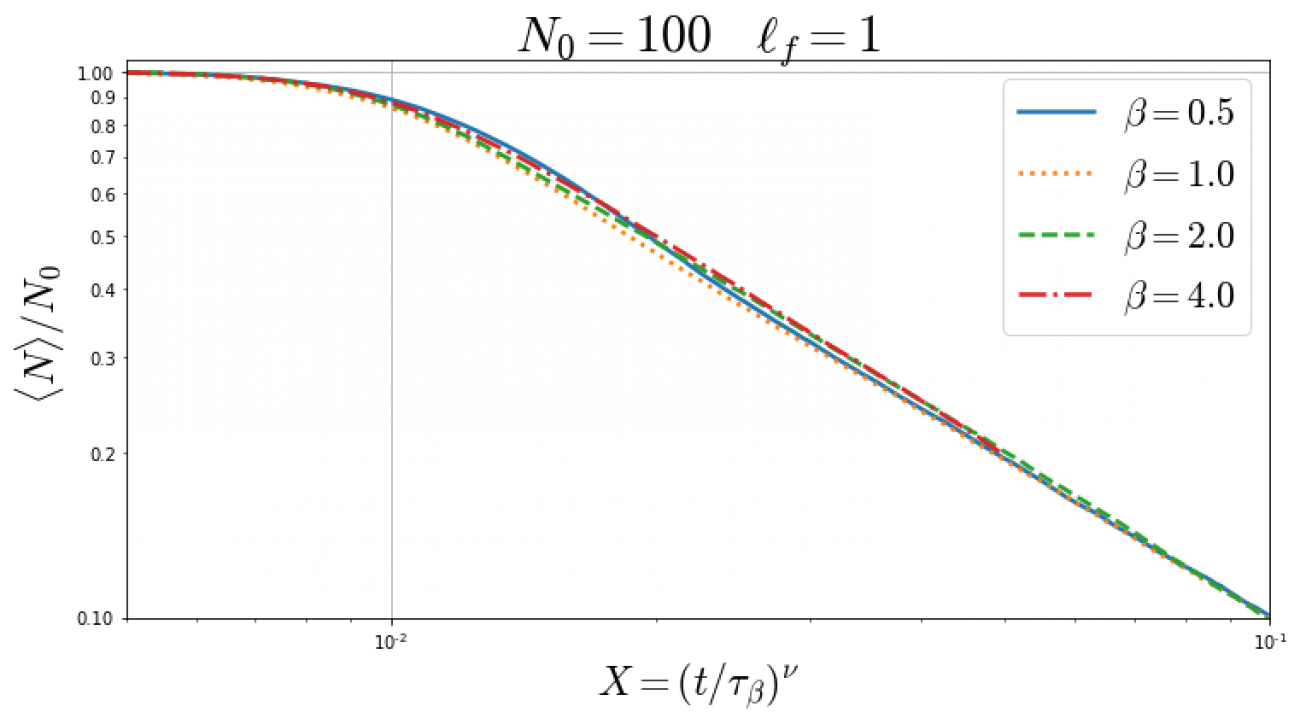
El modelo de fusión de cargas consiste en un sistema de partículas cargadas que se mueven en un dominio circular y tienen una fuerza de repulsión entre ellas de largo alcance. Para complementar la dinámica, las partículas están también sometidas a la agitación térmica caracterizada por una fuerza aleatoria. Si dos partículas se acercan lo suficiente tienen la posibilidad de fusionar conformando una sola partícula con carga compuesta por las originales. Debido a estos eventos de fusión, el sistema permanecerá constantemente fuera de equilibrio mientras el número de partículas disminuye en el tiempo. En este sistema es de interés estudiar la evolución del numero de partículas y sus fluctuaciones. Típicamente se puede esperar una ley de escala para la densidad de partículas en función del tiempo con un exponente a determinar.
Para el estudio de la formación de una doble capa eléctrica, proponemos retomar un modelo simple uni-dimensional del cual hemos estudiado sus propiedades en equilibrio térmico en trabajos anteriores. El modelo consiste en dos partículas “coloidales” cargadas separadas por una distancia L y neutralizadas con N partículas móviles de carga de signo opuesto. Para estudiar los aspectos fuera de equilibrio, se propone una dinámica browniana sobreamortiguada para las cargas móviles y se propone estudiar cómo a partir de una configuración inicial arbitraria el sistema relaja hacia el equilibrio. Entre otras cantidades de interés a determinar está el tiempo de relajación hacia el equilibrio y cómo depende éste de la separación L y el número de partículas móviles N.
