Electric vector potential formulation in electrostatics: analytical treatment of the gaped surface electrode
European Physical Journal Plus 135, 878 (2020)
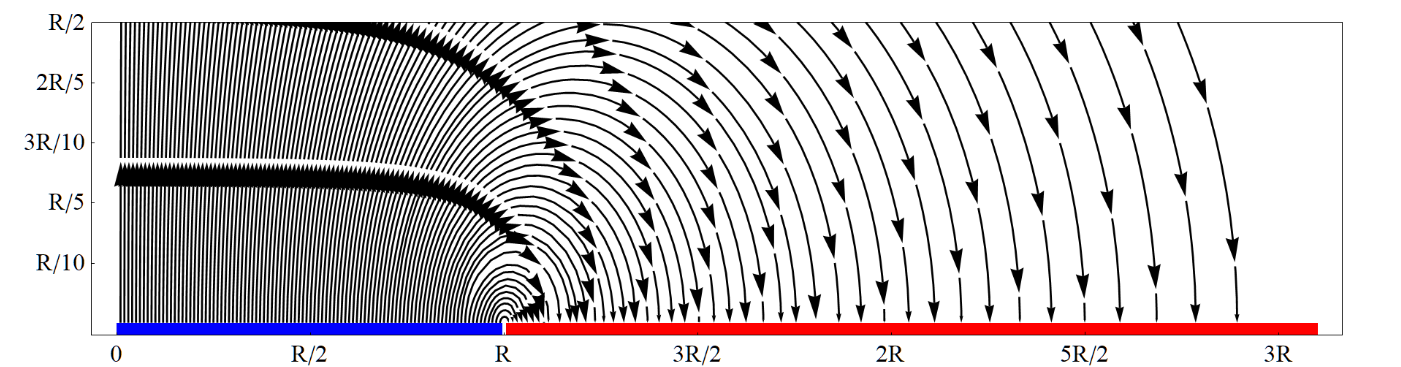
The electric vector potential Θ(r) is a legitimate—but rarely used—tool to calculate the steady electric field in charge-free regions. It is commonly preferred to employ the scalar electric potential Φ(r) rather than Θ(r) in most of the electrostatic problems. However, the electric vector potential formulation can be a viable approach to study certain systems. One of them is the gaped surface electrode (SE): a planar finite region A− kept at a fixed potential Vo with a gap of thickness ν to the remaining grounded field. In this document, the Helmholtz decomposition theorem and the electric vector potential formulation are used to provide integral expressions for the surface charge density and the electric field of the gaped SE of arbitrary contour ∂A. It is shown that the electric field of the gaped circular SE in the R3 space can be obtained from averaging the gapless SE solution over the gap. Even though the approach is illustrated with the circular SE, the strategy could be used in other geometries if the corresponding gapless solution is known. Analytic results are in agreement with numerical approximations of the electrostatic problem via Finite Element Method. Finally, the magnetic analogue of the gaped SE is provided.
Universidad de los Andes | Vigilada Mineducación
Reconocimiento como Universidad: Decreto 1297 del 30 de mayo de 1964.
Reconocimiento personería jurídica: Resolución 28 del 23 de febrero de 1949 Minjusticia.
Web design and programming © Gabriel Téllez
