Self Organized Critical Dynamics on Sierpinski Fractal Lattices
Tesis de pregrado en Física, Universidad de los Andes (2023)
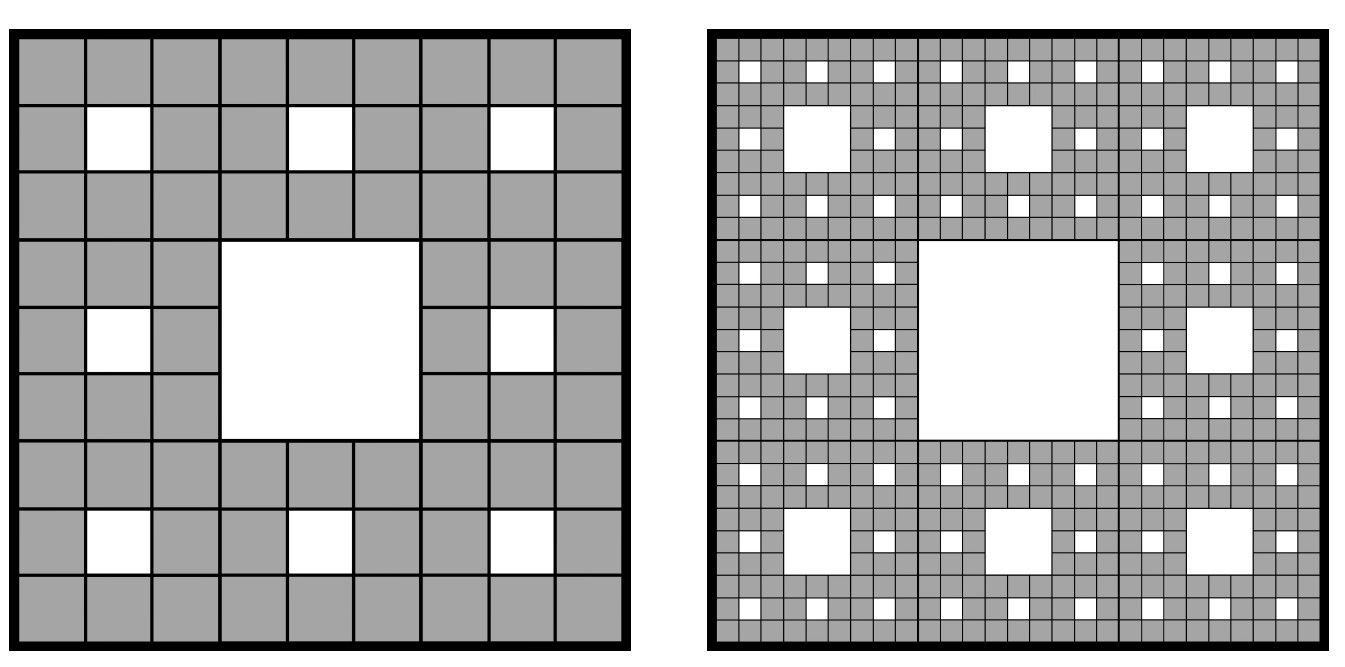
La criticalidad auto-organizada es una propiedad de sistemas dinámicos en los cuales, sin ajustes externos, un sistema evoluciona naturalmente hacia su estado crítico, caracterizado por patrones invariantes a escala y distribuciones de ley de potencias. Esta tesis explora la dinámica crítica auto-organizada en el retículo de la Alfombra de Sierpinski, una estructura que también sigue una ley de potencias en su dimensión, es decir, un fractal. Para lograr esto, se propone un modelo de Ising-percolación como escenario de estudio para la dinámica crítica. Dentro de este marco, se delinea un mecanismo de retroalimentación para la auto-organización crítica, junto con un algoritmo diseñado para implementarlo numéricamente. Los resultados obtenidos del algoritmo demuestran mayor eficiencia en la llegada a la auto-organización crítica en la Alfombra de Sierpinski. Esto es atribuido a la naturaleza iterativa de su construcción y a el impacto que esto tiene en la formación de clusters. El resultado clave de este estudio es una novedosa dependencia de la topología en la dinámica crítica auto-organizada, la cual puede tener diversas aplicaciones en campos relacionados con la transmisión de información.
Universidad de los Andes | Vigilada Mineducación
Reconocimiento como Universidad: Decreto 1297 del 30 de mayo de 1964.
Reconocimiento personería jurídica: Resolución 28 del 23 de febrero de 1949 Minjusticia.
Web design and programming © Gabriel Téllez
