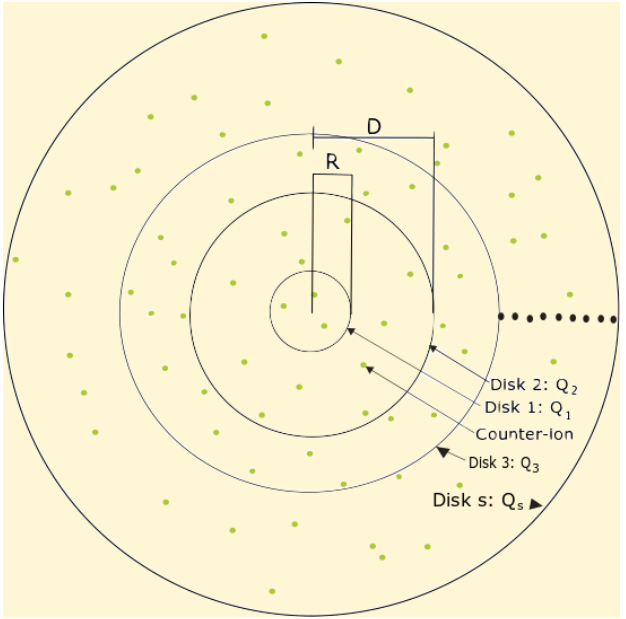
En este proyecto estudiamos algunos aspectos de la mecánica estadística en equilibrio de un plasma de Coulomb bidimensional de un componente clásico (interacción logarítmica) con simetría circular y N partículas puntuales. El modelo presentado es una extensión del estudiado por Mallarino y Téllez. La configuración es tal que hay N partículas con carga q cada una, restringidas a extenderse sobre todo un plano bidimensional, que tiene regiones delimitadas por dos discos cargados tal que Nq-Q1 – Q2 = 0. En este modelo, M contraiones están dentro del área delimitada por el primer disco, adicionalmente hay L iones entre los dos discos y finalmente P afuera del segundo. Enfocamos nuestra investigación en encontrar las funciones de correlación, la carga integrada y la densidad de contacto para una constante de acoplamiento Γ=2, dónde el sistema es exactamente soluble acorde a analogías entre log-gases de Coulomb y la teoría de matrices aleatorias.