Representación de Schrödinger en espacio-tiempo curvo
Tesis de Maestria en Ciencias – Física, Universidad de los Andes (2021)
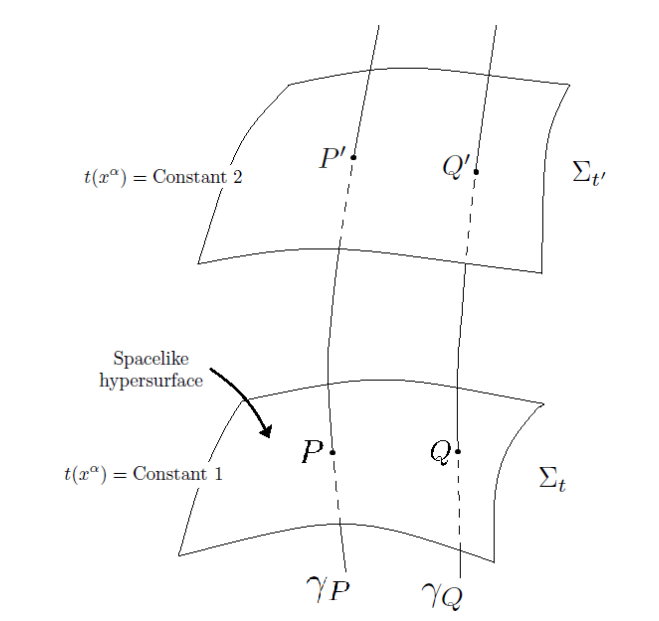
We present a compilation about the Schrödinger representation functional methods in the context of curved backgrounds. Specially, we focus on the representation compatible with the Fock ones. It is known that in QFT on curved space-time there should not be a preferred mode decomposition of the quantized field. This fact, usually is not presented in the naive Schrödinger representation, or at least the preferred modes are putted by hand and there is not a criterion of consistency, in first principles, with the Fock representation. In the paper of [Corichi et al., 2004], an attempt to find the relation between both representations is carried out using the C∗-algebras, specifically Weyl algebras. This article is studied and the formalism required to understand it is developed. Additionally, the relation of the Minkowski, seen as a mixed stated and Rindlers vacuum is studied and displayed in terms of functionals. The
sketch of a possible vacuum different of the constant one is proposed.
Universidad de los Andes | Vigilada Mineducación
Reconocimiento como Universidad: Decreto 1297 del 30 de mayo de 1964.
Reconocimiento personería jurídica: Resolución 28 del 23 de febrero de 1949 Minjusticia.
Web design and programming © Gabriel Téllez
